Home » Data » Weighting data » Regarding de-normalizing and weighting procedures in Stata
| Regarding de-normalizing and weighting procedures in Stata [message #9538] |
Mon, 11 April 2016 06:47  |
AmsP
Messages: 24
Registered: April 2016
|
Member |
|
|
Hello,
I'd like to ask for help about if my procedures to de-normalize and weight data in Stata are correct. I just want to calculate average schooling years of women (older than 30) in urban region whose schooling year is above the average level of all women in the survey.
Step 1: De-normalize each survey (various years) of the same country by "gen v005_denorm=v005*(number of 15-49 aged women in the country in the survey year)/(number of 15-49 women surveyed in this survey round)". After de-normalizing each dataset, I append them together to have a single big survey dataset for this country.
Step 2: gen wgt=v005_denorm/1000000
Step 3: mean v133 [pweight=wgt]
step 4: mean v133 if v133>mean & v025==1 & v012>30 [pweight=wgt] "Here, shall I still add [pweight=wgt]?"
Because I just need a single mean schooling value (for later regressions), I do not think that I need cluster and strata adjustment. Am I right?
But if I do cluster and strata adjustment, then the procedures will become:
Step 1 and 2: the same as above for de-noemalizing, appending and dividing v005_denorm by 1000000
Step 3:gen psu=v021
gen strata=v023
svyset psu [pweight=wgt], strata(strata)
Step 4: svy: mean v133
Step 5: svy: mean v133 if v133>mean & v025==1 & v012>30
The two methods generate the same result (I do not need to consider standard error, so I prefer the first method without cluster/strata adjustment).
Thank you very much in advance!
[Updated on: Mon, 11 April 2016 06:57] Report message to a moderator |
|
|
|
| Re: Regarding de-normalizing and weighting procedures in Stata [message #9564 is a reply to message #9538] |
Mon, 18 April 2016 11:21   |
 Bridgette-DHS
Bridgette-DHS
Messages: 3230
Registered: February 2013
|
Senior Member |
|
|
Following is a response from Senior DHS Stata Specialist, Tom Pullum:
If you multiply all the weights by a constant, you will not alter any of the usual estimates--means, proportion, regression coefficients, etc. I suggest that you try it, using iweight or fweight, and do a comparison.
Moreover, in any operation with pweight, Stata will automatically re-normalize so that the total number of weighted cases equals the total number of unweighted cases. That's why you will get exactly the same means, proportions, regression, coefficients, etc., using pweight=v005 or pweight=v005/1000000. You may think you are de-normalizing v005, but pweight will always re-normalize. Again, try it and compare results.
I would describe the weights you propose as "inflation weights". You would use them to inflate to the total population. You could do this if you want to estimate, for example, the NUMBER of women whose last birth was in a facility, etc. (For this purpose you do need to divide v005 by 1000000.) I would not recommend using inflation weights to inflate to the total population, but that's up to you.
If you are planning to make this adjustment and then pool surveys, you will have to expect that countries with a large population will completely dominate the analysis. The pool of all surveys will be normalized but the weighted subtotals will be in proportions to the population sizes.
I agree with you about not making the adjustments for clustering and stratification, unless you will be using the standard errors. Those adjustments only affect the standard errors, not the estimates.
|
|
|
|
| Re: Regarding de-normalizing and weighting procedures in Stata [message #9643 is a reply to message #9564] |
Thu, 28 April 2016 07:03   |
AmsP
Messages: 24
Registered: April 2016
|
Member |
|
|
Thank you very much! I compare the results of using pweight, iweight and fweight. Pweight and iweight allow to use de-normalized v005/1000000, but fweight only allows to use de-normalized v005 (Stata points out that fweight has to be an integer). I am attaching the picture of the results.
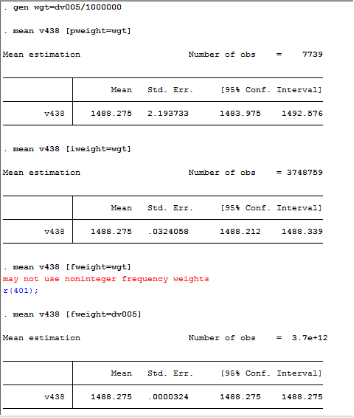
The means are the same across the three results (this is the only value that I need), and the standard errors and confidence intervals are different. So does it mean that I can stick at using pweight?
But I do not know why the number of observations are different among the three weights. The number of observations in pweight result is equal to the number of women in the survey (7739), while the number of observations in the iweight result is equal to population size (3748759).
Additionally, I have two more questions, and I hope to have your answers.
Firstly, for sampled women whose given variable is missing (e.g. 9999) and blank ("."), I just simply drop them before weighting manipulation. Is this correct?
Secondly, may I always use the same weight (in my case de-normalized v005/1000000) for calculating means of a given variable for sub-population groups (e.g. urban/rural, different provinces, or different age groups)?
Thank you very much again!
-
 Attachment: Foto 1.png
Attachment: Foto 1.png
(Size: 38.06KB, Downloaded 2343 times)
[Updated on: Thu, 28 April 2016 07:05] Report message to a moderator |
|
|
|
|
|
| Re: Regarding de-normalizing and weighting procedures in Stata [message #9658 is a reply to message #9655] |
Fri, 29 April 2016 15:26   |
AmsP
Messages: 24
Registered: April 2016
|
Member |
|
|
Thank you very much!
Dr. Pullum suggested not to de-normalize the data. But because I pool various surveys of a given country into one single dataset, I think I need to first de-normalize them. So am I right?
Just one more and the final question (sorry for so many questions), I simply drop all interviewed women with missing value of a given variable before weighting (but after de-normalizing), is this OK?
[Updated on: Sat, 30 April 2016 13:41] Report message to a moderator |
|
|
|
| Re: Regarding de-normalizing and weighting procedures in Stata [message #9698 is a reply to message #9658] |
Mon, 09 May 2016 06:29  |
 Bridgette-DHS
Bridgette-DHS
Messages: 3230
Registered: February 2013
|
Senior Member |
|
|
Following is a response from Tom Pullum:
There have been previous emails on what to do with the weights when you pool surveys. There are basically two options. The first is to re-scale the weights so that each survey counts equally. That is, if you have 15 surveys and the total number of cases in these 15 surveys is N, then you multiply v005 (or hv005) by whatever number will give a total weight of N/15 for each survey (and then scale up by a factor of 1 million to get rid of decimals). The second option is to rescale so that the total weight for each survey is proportional to the population of the country, or the number of women 15-49 in the country, etc., at the time of the survey.
In terms of the two houses of the U.S. Congress, the first option is like the Senate, because each state counts equally (each state gets two senators). The second option is like the House of Representatives, because the number of representatives allowed for each state is proportional to the population of the state.
I think REnormalization is a more accurate description than DEnormalization....
|
|
|
|
Goto Forum:
Current Time: Thu Jul 10 13:51:51 Coordinated Universal Time 2025
|
 The DHS Program User Forum
The DHS Program User Forum
 Members
Members Search
Search Help
Help Register
Register Login
Login Home
Home








